

In the case of physical principles, some of these will be just reliable observations.įermat's Least Time Principle tells us that light take the least time path between possible trajectories. ↑ Ben-Menahem, A., Historical Encyclopedia of Natural and Mathematical Sciences, Springer Science & Business Media, 2009.A proof requires axioms, basic statements that can't be proven. V., “New view on the diffraction discovered by Grimaldi and Gaussian beams”, arXiv preprint arXiv:1302.6287, 2013. ↑ Grunenberg, J., Computational Spectroscopy: Methods, Experiments and Applications, John Wiley & Sons, 2011. R., Aristotle’s journey to Europe: A synthetic history of the role played by the Islamic Empire in the transmission of Western educational philosophy sources from the fall of Rome through the medieval period, ProQuest, 2007. ↑ Ronchi, V., Rosen, E., Optics: The Science of Vision, Courier Corporation, 1991. S., Learning Higher Mathematics: Part I: The Method of Coordinates Part II: Analysis of the Infinitely Small, Springer Science & Business Media, 2013.
#Angle of incidence equals angle of reflection... archive
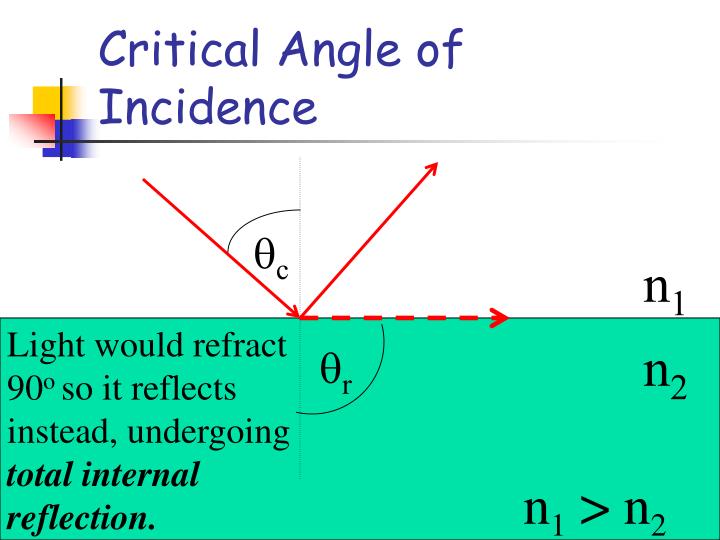
M., Archive for history of exact sciences 1982, 26, 221–240. F., Livesey, S., Wallis, F., Medieval Science, Technology, and Medicine: An Encyclopedia, Routledge, 2014. L., The Britannica Guide to Algebra and Trigonometry, The Rosen Publishing Group, 2010. I., Theories of Light: From Descartes to Newton, CUP Archive, 1981. M., Descartes’s Theory of Light and Refraction: A Discourse on Method, American Philosophical Society, 1987. C., The Beginnings of Western Science: The European Scientific Tradition in Philosophical, Religious, and Institutional Context, Prehistory to A.D. C., Theories of Vision from Al-kindi to Kepler, University of Chicago Press, 1981. This causes the colours to be reversed and produces visible light at about 52°-54°. In the case of a double rainbow, secondary bows are caused by double reflection inside the raindrop. This is why you will never be able to reach the end of a rainbow. Other angle, and so when you move, the rainbow moves with you. The set of all the raindrops that can be seen from this angle at once forms a cone pointing towards the Sun.

To see sunlight that has passed through a raindrop, there needs to be an angle of about 40°-42° between you, the raindrop, and the Sun. Theodoric showed that the light of the Sun is refracted, and then internally reflected, inside each drop. Theodoric did this by experimenting with spherical flasks, which he filled with water to represent raindrops. The German philosopher Theodoric of Freiberg (also known as Dietrich of Freiberg) explained how rainbows are formed in about 1307. The English philosopher Roger Bacon, who was one of the earliest European advocates of experimental science, reviewed Al-Haytham’s Book of Optics in 1267, and it was translated into Latin shortly after. This was mainly due to increased contact with the Islamic world. Science began to progress again in Europe after the Renaissance of the 12th century. This led him to suggest that vision occurs in the brain, rather than the eyes and that it is, therefore, subjective. He likened it to a camera obscura, a pinhole camera, and so suggested that images must also be inverted in the eye. Vision occurs when the Sun’s rays are reflected from objects and into our eyes.Īl-Haytham experimented with the laws of reflection and refraction using different shaped mirrors and lenses, and he accurately described how the eye functions as an optical instrument. Al-Haytham stated that light consists of tiny particles of energy that travel in straight lines and emanate from the Sun at a large but finite velocity. The Iraqi mathematician Ibn al-Haytham (also known as Alhazen) was the first person to correctly describe how perception occurs in about 1021 when he proved that light enters, but is not emitted by, the eye. Ī plot showing sin( θ), cos( θ), and tan( θ). Sin, cos, and tan waves could not be represented graphically until after the invention of the Cartesian coordinate system by Descartes and the French mathematician Pierre de Fermat in 1637. Hipparchus’ work was referenced by Ptolemy over 250 years later, and so it’s not known why he didn’t derive the sine law of refraction himself. The ancient Greek astronomer Hipparchus created the first documented table of sine functions before 125 BCE. Tan( θ) = opposite length / adjacent length In the triangle above, sin( C) would equal length c / length c, which equals 1. The sine of 90° is 1 because the opposite length will also be the longest, the hypotenuse. In Figure 2.3, sin( A) = length a / length c The sine of an angle ( θ) equals the ratio of two lengths - the length opposite the angle, and the longest length, the hypotenuse. The sine function shows how the angle inside a triangle changes as the lengths of its sides change. Reflection, Refraction, and DiffractionĢ0.


 0 kommentar(er)
0 kommentar(er)
